High school
-
CalculusIf you are having problems with Year 12 or 13 Calculus then read this 45 page booklet. There are no exercises but a lot of worked examples on Finding the Derivative, Differentiating with Respect to Other Variables, Rates of Change, Equations of Tangents, Increasing and Decreasing Curves, Stationary Points, Determining the Nature of Stationary Points, Curve Sketching, Closed Intervals, Graphs of Derivatives and Optimisation, Preparing to Integrate, Differential Equations, Definite Integrals, Geometric Interpretation of Integration, Areas between Curves and Integrating along the y-axis.
-
Year 13, Differentiating by First PrinciplesDifferentiation is about rates of change for example, the slope of a line is the rate of change of y with respect to x. To find the rate of change of a more general function, it is necessary to take a limit. This is done explicitly for a simple quadratic function.
-
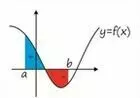
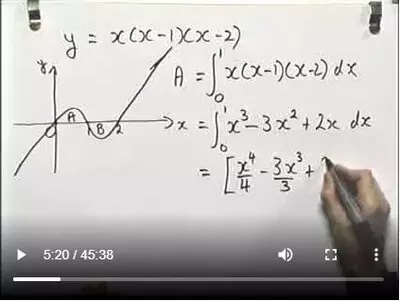
Year 13, Areas by IntegrationIntegration can be used to calculate areas under a graph. In simple cases, the area is given by a single definite but in more complicated cases the correct answer is obtained by splitting the area into several parts and adding or subtracting the appropriate integrals.
-
Year 13, The Quotient RuleThe quotient rule is a special rule that may be used to differentiate the quotient of two functions.